Self Driving RC Car
March 2022

Overview
In our Robotic Vision class, the big assignment was to program an RC-car to self-driving using only a camera,
wheel odometry and an IMU. There were 3 students per car and our grade would be determined by how fast our car
performed against our peers, including a race around the track.
The track consisted of blue and green pool noodles strung together to create an inner and outer loop. To add
to the complexity, orange cones were added as additional barriers.
The robot platform was built upon a Traxxas 4WD RC car. The car was equipped with a simple motor encoder, an
Intel Realsense D435 Stereo Depth Camera with an IMU, and computation was run off an Nvidia TX1.
Our team implemented a fast and accurate path planning algorithm that finished with the 2nd best time in the
class.
My Contributions
We took a unique approach in how we worked together to program our robot. We worked together to extract
images, then the 3 of us diverged to each develop a path planning algorithm. We would bounce ideas off each
other and integrate aspects of each other’s code as we optimized for speed and accuracy.
To process the images, we broke the image into hue, saturation, and value (intensity) values. We then
performed a binarized thresholded to the blue and green hue channels to detect where the pool noodles were. We
did the same for the red channel to find the cones. Performing a bitwise OR on the 3 images we had a combined
image where only the obstacles appeared with high values. We then resized this image into a much smaller
format (about 60x100 pixels) to make computation easier.
One team member designed a reactive navigation system that would assign a turn values to a grid, and at each
timestep would choose the max turn value (i.e. prioritize objects closer to the car that would necessitate
turning more to avoid an obstacle) His approach was the fastest at driving when there were no cones on the
track, however my approach worked the best at avoiding cones as well as deciding when it was necessary to back
up.
My approach was to try to actually path plan given what we can see ahead of the car instead of a reactive
approach as used by many in the class. Sadly, the Nvidia TX1 we
were using was already bogged down with a lot of unnecessary overhead so very little computation could be
done. Because of this, I was unable to perform a gradient-based optimization but was able to perform a simple
greedy operation. I began by creating a Euclidian distance map where each value in the array was the minimum
distance to an obstacle, whether that being the wall or a cone. At each time step I would run two greedy
algorithms, a local and global. Each algorithm would find the minimum point at a certain y value, however the
local algorithm was constrained to be within a certain x distance of the previous location. The purpose of the
global approach was to help the local not get stuck in local minimums which was typically the case. Generally
the global algorithm would find points along a line, I would filter the noisy points and find a line of best
fit with least squares that was weighted with a single point in the center of the image. This kept the
algorithm mostly pointing in the right direction. I would then calculate a steering angle by weighting the two
slopes of the local and global greedy algorithm.
With our third teammate I wrote the backup script. Interfacing with the wheel odometer proved to be difficult
so we simply pulled the IMU values from the RealSense camera. We had two cases for backing up, the first being
when the IMU values would be below 0.1 for 10 frames (the camera was running about 15 frames a second) This
mostly worked, however every once in awhile when the car would hit top speed without turning, the IMU would
zero out and trigger a backup, this generally wasn’t the case though when there were cones on the track. The
2nd case for backing up was done using the Euclidian distance map with the points found by the local greedy
algorithm. If the points ahead were below a certain threshold, i.e. there’s obstacles ahead with no clear path
around them, we would back up and try again now having a better view of what’s ahead.
We found that this algorithm performed best when avoiding obstacles and could always navigate its way out of a
tight corner. In the class competition, we tied for the fastest overall time with no obstacles and got 3rd for
the fastest time with cones. We would’ve been second, however we hit a cone and were assessed a time
violation. The final challenge was a single elimination bracket 1v1 race. Our car won the quarter and
semi-finals advancing to the championship race where we lost to the better team. The other team came up with
the novel idea of looking for the carpet instead of the obstacles. Doing so was much simpler and allowed them
to process more frames per second allowing them to navigate better around turns where a slower framerate
hindered performance.

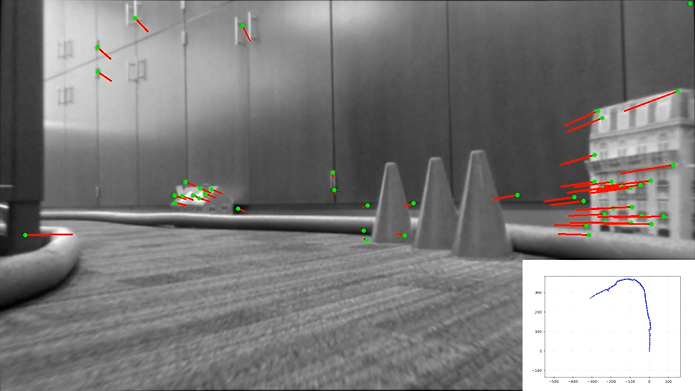
This is a single frame from the car, the processing pipeline is shown below.

Binarized thresholded image of blue, green, and red channels that only shows the track and obstacles

Binned down image. The euclidian distances are calculated from this smaller image
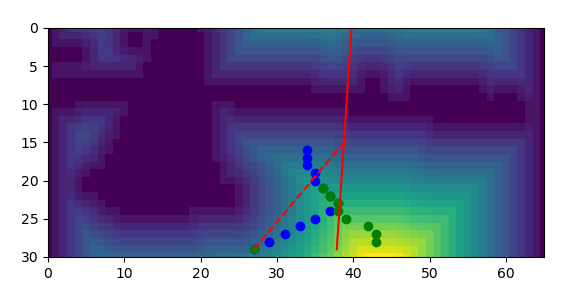
Greedy algorithm searching for optimal path in the euclidian distance map. The darker colors are lower values and the brighter colors are higher. The blue dots are the local greedy algorithm, green is the global, red is line of best fit and dashed red is the calculated steering angle. The steering angles were passed into a PD controller that helped limit turning oscillations.
Things I Learned and Skills Developed
This was a fun and competitive project to work on with friends. I learned some simple path planning algorithms as well as tricks and techniques to optimize processed frames per second. We had to mindfully program as we were running on limited processing power and come up with unique solutions to avoid potential cone traps as arranged by our professor.
Code
Code will be shared at a later date